Hello,
I’ve been doing a little research into anti-matter and anti-hydrogen and the experiments being undertaken with them.
I’d just like to ask,
What kind of scientific advancements could be made by examining how anti-hydrogen reacts? and, With new technologies could we create other anti-atoms?
Thank you for your time, Christopher.
Svar:
The study of anti-hydrgen is mainly aimed at determining if there are differences between that and ordinary hyrogen on a quantum mechanical level. E.g. if the constants of nature are the same. On a maybe much deeper level we need to find out why we are here! The Standard Model (Big Bang) model of the Universe predicts that during the very first fragments of a second of the story of the Universe equal amounts of matter and anti-matter ought to have been created. Most of the matter and anti-matter seems to have disappeared due to mutual annihilation. What we would very much like to know, Thank You, is why there was a slight difference in the balance, causing a tiny bit of matter to be left over – the 5% matter that we consist of to-day.
In principle other anti-atoms might be produced in the large accelerators like LHC at Cern, but it requires enormously higher energies that what presentlys is available. Only the future will see if and when we might be able to construct even larger machines for this. Best, OJK.
Hej brevkasse. Jeg er en dreng på 14, som er ret interesseret i den fysiske og kemiske videnskab. Og jeg har undret mig i lidt tid over hvorfor der i det periodiske system er to grupper (Lanthanider og Actinider) som ligesom er smidt ud af systemet. Håber på at du kan forklare mig det, og gøre mig den smule klogere.
Venlig hilsen LL
Hej LL.
Jeg kan godt forstå at du undrer dig over det, for det er også en lille smule besynderligt og afviger lidt fra det system, der ellers gælder i resten af det periodiske system.
Det periodiske system er, som du sikkert ved, bygget op, så grundstoffer, der har samme antal elektroner i den yderste skal, står oven over hinanden i kolonner. I praksis betyder det også, at elementerne ender sammen i grupper, hvor der puttes elektroner i den samme type orbital, efterhånden som atomnummeret stiger. Orbitaler er forskellige typer pladser i skallen, og dem kalder man henholdsvis s, p, d, og f orbitaler. I den tynde gruppe til venstre fyldes der elektroner i en s-orbital, i gruppen helt til højre fyldes de i en p-orbital, og i den store gruppe i midten er det en d-orbital der fyldes i. Efter d-orbitaler kommer f-orbitaler, og de begynder at blive fyldt op i 6. række i det periodiske system.
Hvis fysikkens love fulgte det periodiske system perfekt, skulle f-orbitalen fyldes efter s-orbitalen var blevet fyldt i 6. række. Dvs. hvis du kigger på grundstof 56 (Ba) der lige har fået den anden elektron i sin 6. s-orbital, så burde det næste grundstof, grundstof 57 (La), få den første elektron i sin f-orbital. Men det sker ikke. I stedet ender der en elektron i d-orbitalen i grundstof 57 (La), og La hører altså derfor hjemme i samme kolonne som Sc og Y, der begge også har netop én elektron i den yderste d-orbital. De næste 10 elektroner (fra grundstof 58 til 71) kommer i f-orbitalen som vi forventede før, men eftersom den ene elektron der kom i d-orbitalen til at starte med, er den elektron, der er i den yderste skal, hører alle disse grundstoffer også til i samme kolonne som Sc og Y. Disse stoffer kaldes Lanthaniderne. Det samme sker for grundstof 89 (Ac), der i stedet for at få sin første elektron i f-orbitalen får den i en d-orbital og derefter fyldes f-orbitalen op. Disse stoffer hører derfor også til i kolonne med Sc og Y og kaldes for Actiniderne. Da det er upraktisk at tegne alle disse stoffer i denne kolonne, flytter man dem ud for sig i stedet for, når man tegner det periodiske system.
Det skal lige nævnes, at der er undtagelser blandt Lanthaniderne og Actiniderne. F.eks. følger grundstof 61 (Pm) ikke vores system, og har derfor 5 elektroner i f-orbitalen i stedet for 1 i d-orbitalen og 4 i f-orbitalen, som vi forventer. Der er flere lignende undtagelser i Actiniderne.
Tak for spørgsmålet. Jeg håber du blev klogere. Hvis du vil vide mere kan du prøve at kigge på denne hjemmeside, der dog er på engelsk:
Mvh. Thorbjørn Villesen, ph.d.-studerende.
Keith Enevoldsen fra USA har tegnet en rigtig flot udgave af grundstoffernes periodiske system, og jeg har fået lov at oversætte planchen til danske.
Den kan bruges helt frit, men lad venligst være med at ændre den.
ojk
Hej!
Nogle nuklider er jo radioaktive ved K-indfangning, hvor kernen snupper en elektron fra K-skallen. Men hvad nu, hvis nukliden befinder sig i et plasma, der er så varmt, at der slet ikke er bundne elektroner. Er det så stabilt, eller vil kernen reagere med en elektron i plasmaet? Kommer halveringstiden så ikke til at afhænge af elektrontætheden?
Jeg tænker specielt på nukliden Be-7, som dannes i små mængder ved Big Bang-kernesyntesen. Det har ifølge Databogen en halveringstid ved K-indfangning på 53.3 døgn, altså en meget høj værdi sammenlignet med tiden for syntese. Så hvornår henfalder dette Be-7? I løbet af nogle måneder eller år, eller sker der først langt senere, når det bliver koldt nok til, at elektroner kan holdes i en skal?
Hilsen HN.
Kære HN.
Du har helt ret. Be-7 henfalder først meget senere, når det bliver koldt nok til, at elektroner kan holdes i en skal. Det sker efter cirka 500 år, når Universets temperatur er faldet til 100.000 grader Celsius svarende til en termisk energi på 10 eV. I princippet kan Be-7 også henfalde tidligere ved at indfange en elektron direkte fra plasmaet, men som du allerede har gættet, afhænger denne process af elektrontætheden - og i det tidlige univers var tætheden meget lav, så sandsynligheden for at indfange en elektron direkte fra plasmaet var forsvindende lille. (Derimod spiller direkte elektron-indfangning en vigtig rolle i solens indre, hvor tætheden af plasmaet er høj.
Halveringstiden af Be-7 i solens indre er cirka 140 dage, næsten tre gange længere end halveringstiden af atomart Be-7.)
Mvh.
Oliver Kirsebom
Postdoc
Institut for fysik og Astronomi
Aarhus Universitet
Hej Spørg IFA,
Grunden til at fotoner bevæger sig med lysets hastighed, er at de ingen masse har og derfor ikke vekselvirker med Higgs-feltet.
Jo mere en partikel vekselvirker med Higgs-feltet, jo mere ”bremses den”.
Gluoner har ingen masse heller, så burde de ikke også bevæge sig med lysets hastighed?
Mvh KM
Hej KM,
Du har helt ret, at en fri gluon ville bevæge sig med lysets hastighed. Problemet med gluoner er bare, at de kun findes i nærheden af andre gluoner eller kvarker. Den stærke kraft har den egenskab, at man ikke kan isolere hverken gluoner eller kvarker. Gluonerne er derfor altid bundet inde i systemer med masse, som derfor ikke bevæger sig med lysets hastighed.
Mvh
Hans Fynbo
Lektor, Institut for Fysik og Astronomi
Hej Spørg IFA.
Jeg ville gerne vide hvad ”Thomson røret” er? Jeg lærte det for mange år siden da jeg gik i folkeskole. I dag kan jeg kun huske at det skulle være noget med hvordan protoner – elektroner – neutroner opfører sig.
Med venlig Hilsen
HJK
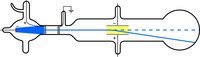
Svar:
Thomson røret er et glasrør med indlejrede elektroder, som vist på billedet. Det er pumpet fri for luft. I foråret 1897 brugte J. J. Thomson, der var professor på Trinity College, Cambridge et sådant rør til at vise at de såkaldte ”Katode stråler", man havde opdaget tidligere, kunne afbøjes i et elektrisk felt, og ved at observere denne afbøjnings størrelse kunne Thomson komme frem til en værdi for forholdet mellem elektronens masse og dens ladning. Han fik Nobel prisen i 1906, bl.a. for dette arbejde.
en.wikipedia.org/wiki/J._J._Thomson
Venlig hilsen
Helge Knudsen
Lektor, IFA
Hejsa,
Mine spørgsmål er således:
Hvordan kan en partikel som fx. en kvark være elektrisk ladet, når den hverken er en elektron eller har en elektron. For 'elektricitet' er jo i sig selv fritløbende elektroner, ik? Har det noget med deres spin at gøre?
Vh
KM :-)
Kære KM.
Elektronen har ganske rigtigt en elektrisk ladning. Den er -e, som læses minus en elementarladning (elementarladningen forkortes med e, hvilket kan være lidt forvirrende fordi vi også tit bruger e for elektronen). Elektrisk ladning er altså en egenskab en partikel kan have og ikke noget, som er specielt for elektronen.
Naturens byggesten er atomer, som er neutrale, dvs. totalt set har de ingen elektrisk ladning, men de består af ladede partikler. Atomet består af en meget lille kerne (ca. 10^-15 m) med positiv ladning, som er omkredset af de negative elektroner i en radius på ca. 10^-10 m (atomet er altså ca. 100.000 gange større end selve kernen). For at atomet skal være neutralt, må kernen altså være lige så positiv, som det samlede antal elektroner er negative. Det, der gør kernen positiv, er protonerne. En proton har ladningen +e (plus en elementarladning). Inde i atomkernen er der også neutroner, som ikke har nogen elektrisk ladning. De fungerer som en slags lim, der opvejer den frastødende elektriske kraft, som er imellem protonerne. Protonen og neutronen er ca. lige tunge og er ca. 2000 gange tungere end elektronen, så stort set hele atomets masse sidder i atomkernen. Antallet af protoner er det, der afgør hvilket grundstof vi ser på, fx har kobber 29 protoner i kernen, og et neutralt kobber atom har derfor 29 elektroner, der omkredser kernen.
Elektronerne er bundet til kernen af den elektromagnetiske kraft, akkurat som planeterne i solsystemer er bundet til Solen af tyngdekraften. De elektroner, som er længst fra kernen, er svagest bundne og kan derfor lettest rives af atomet. På den måde bliver atomet totalt set positivt, da der nu er færre elektroner end protoner, og man kalder det i stedet for en ion (man kan også have negative ioner, hvor atomet i stedet har fået tilføjet elektroner).
Elektricitet er bevægelse af elektrisk ladning. Det kan både være positiv eller negativ ladning, og er altså ikke kun bevægelse af elektroner. Tit er det dog elektronerne som bevæger sig, da disse er meget lettere at flytte end ioner, som er tunge pga. den tunge atomkerne.
Spin er også en egenskab, partikler kan have. Det svarer til rotation omkring en indre akse, som fx Jordens rotation. Når noget roterer om en akse kan det enten dreje den ene vej eller den anden, og man har derfor to tilstande. Når man snakker om partikler, som fx elektronen, kalder man det spin op eller spin ned, og det illustreres oftest med hhv. en pil op eller en pil ned.
En kvark er en partikel ganske som elektronen. Elektronen er det man kalder en elementarpartikel, som betyder at den ikke kan splittes op i mindre dele. Man skulle tro, at elementarladningen så var den mindste ladning, man kan have, og det troede man også, indtil man fandt kvarken. Man fandt nemlig ud af, at protonen (som man indtil da også havde troet var en elementarpartikel) var sammensat af tre endnu mindre partikler, som man kaldte for kvarker. Da protonen jo har ladningen +e, så må de tre kvarker tilsammen også have ladningen +e. Man fandt ud af at protonen bestod af to typer af kvarker: up-kvarken og down-kvarken, som har en ladning på hhv. 2/3e og -1/3e (navnene her har ikke noget at gøre med spin op og ned). For at dette giver +1e må protonen altså bestå af to up-kvarker og en down-kvark. Neutronen består også af tre kvarker: en up-kvark og to down-kvarker. Tilsammen fås dermed en ladning på 0.
I dag ved vi at der findes i alt seks kvarker: up, down, charm, strange, top og bottom. Up, charm og top har alle ladningen 2/3e og down, strange og bottom har ladningen -1/3e. Elektronen er også en del af en type partikler, som vi kalder leptoner. Der findes tre leptoner: elektronen, myonen og tau-partiklen, som alle har ladningen -1e.
Mvh
Gunvor T. Koldste
Ph.d.-studerende
Hej Jeg har længe gået med en tanke som jeg forgæves har forsøgt at finde svaret på, så nu prøver jeg her.
Det er en rimelig abstrakt tanke, men jeg prøver at formulere det så konkret som muligt.
Hvis jeg forestiller mig at jeg bliver større. Altså vokser til en størrelse hvor det synlige univers for mig ville være på størrelse med f.eks en knappenålshoved. Ville universet for mig så ikke blive et fast stof? Altså når jeg vokser mindskes afstanden mellem de fysiske objekter i universet, og jeg tænker, at på et tidspunkt ville afstanden for mig blive så lille, at jeg ville opfatte det som et fast stof.
Hvis jeg altså blev så stor, at afstanden mellem galakser for mig f.eks svaret til 1/1000 del af en millimeter, ville det så for mig opfattes som fast stof?
Håber ikke spørgsmålet er for absurd.
Mange hilsner
Michael
Den tanke dukker op i forskellige varianter med jævne mellemrum. Ole Sarvig har skrevet digtet Vågen Nat om emnet.
Svaret er nej.
Grunden er for det første, at der er meget længere imellem stjernerne i forhold til deres størrelse end imellem atomkernerne i forhold til atomernes størrelse. I fast stof ligger atomerne tæt op ad hinanden, og de er omkring een milliardedel i diameter. Gennemsnitsafstanden imellem stjernerne i vores nærhed er omkring 10 lysår, og en typisk stjerne er 1 million km i diameter, og har et planetsystem, som er omkring 300 milliarder km i diameter. Atomerne er “kun" nogle hundrede tusinde gange større end atomkernerne. Hvis du tog de meget store syvmilestøvler på, så afstanden mellem stjernerne skrumpede til noget, der svarer til afstanden imellem atomerne, ville planetsystemerne blive alt for små i forhold til afstanden imellem deres stjerner; omkring 340 gange, så dit "faste stof” ville i det tilfælde være meget løst; som en meget tynd gas. Den anden grund er, at vi føler stof som fast fordi elektronskyerne i vore fingre og i det faste stof vekselvirker elektrisk - vi frastødes, så vi ikke kan bore fingrene ned i stoffet. Imellem planetsystemerne er der ikke en tilsvarende kraft. Galakserne er forholdsvis tættere på hinanden i forhold til deres diametre, men der vil stadig være rigeligt med plads til at du kan stikke syvmilefingrene lige igennem uden at føle noget fast.
Hej jeg er i gang med at skrive srp, og en del af min opgaveformulering lyder: Du skal udregne hvor meget energi, der udløses i en enkelt fissionsproces og dermed også hvor meget masse der skulle til, for at en atombombe havde en sprængkraft ækvivalent til 20 kiloton TNT.
Min tanke er et beregne Q for en enkelt fissionsproces for Pu, og så herefter finde hvor meget energi, der frigives for 1 gram plutonium, for igen at kunne gange dette op til den sprængkraft, som jeg er blevet bedt om at finde den tilsvarende masse til. Jeg tænker at sammenligne med bomben Fat Man som netop var en plutoniums bombe med en sprængkraft på ca 20 kiloton TNT. Jeg er dog ikke sikker i min fremgangsmåde, og ville hører om du ville fortælle mig om dette kan lade sig gøre og hvad formlen for at finde den energigevinst for 1 gram Pu er
Mvh Kamilla
Hej Kamilla,
For at finde energien frigivet ved neutron induceret fission at 239Pu skal vi se på reaktionen:
n+239Pu -> A1Z1+ A2Z2, hvor A1Z1 og A1Z2 er fissions produkterne. I virkeligheden er der en fordeling af forskellige fissions produkter, men vi kan antage, at der er tale om symmetrisk fission – dvs A1=A2 og Z1=Z2.
For at det går op, må A1=A2=120 og Z1=Z2=47 – dvs 120Ag.
Din første opgave bliver at finde masserne af n, 239Pu, og 120Ag. Energien frigiver per 239Pu er da Qfission=( M(n)+M(239Pu) – 2*M(120Ag) ) * c2
Det burde give ca. 200 MeV. Hvis du er rigtig ambitiøs kan du også prøve at regne på, hvad Qfissionbliver, hvis produkterne er forskellige (asymmetrisk fission). Forskellen er nok ikke særlig stor.
Din næste opgave bliver at finde, hvor energi, der frigives ved sprængning af 2 kilotons TNT – i Joule og MeV, hvs du nu foretrækker. Lad os kalde det tal for ETNT.
Så finder du antal fissioner af 239 nødvendig ved forholdet mellem de to tal – husk at regn i samme enheder for de to tal. Lad os kalde tal for N.
N = ETNT /Qfission.
Det sidste, du mangler, er nu blot at regne N om til en masse i gram. Det gør du ved at bruge den molære masse af 239Pu, der er ca. Mmolar = 239 g/mol (slå den rigtige værdi op).
M = N / NA * Mmolar
Her er NA Advogadros tal.
Alternativt kan du bare finde massen af et 239Pu atom i gram. Så er
M = M(239Pu) * N
Det må være den nemmeste vej til at løse problemet.
Mvh, Hans Fynbo
Professor of experimental nuclear physics