
Cavity Quantum Electrodynamics (CQED) is an attractive platform for the realization of efficient light-matter quantum interfaces at the single photon level. Such interfaces are key elements for the development of quantum information and communication science due to the need for swapping information between flying and stationary qubits [1,2,3].
Clouds of cold ions are an interesting alternative system to a single atom/ion for studying CQED effects. When trapped and cooled below a critical temperature, ions form a spatially ordered state, referred to as an ion Coulomb crystal.
Those ion Coulomb crystals have a series of attractive solid state properties of relevance for CQED studies and for the development of quantum information devices. One is the uniform density of the crystalline structure, where the ions are positioned at distances of ~10 mm [5,6], which leads to neither temporal nor spatial inhomogeneous spectral broadening, due to the lack of close ion-ion interactions. Another is the stable trapping for hours, which allows for repeatable experiments with a coupling strength being constant to within a few percent.
At the quantum level, the interaction of light and matter is based on the exchange of single excitations between atoms and a single mode of the electromagnetic field. Cavity quantum electrodynamics (CQED) focuses on the understanding of this interaction when the light field is confined inside a cavity [7].
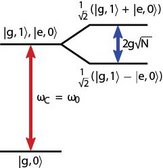
Within CQED the regime where the coherent process, namely the rate at which a single excitation is exchanged between matter and light field, exceeds both the decay rate of the dipol, ?, and the decay rate of the cavity light field inside the cavity, ?. In the case of an ensemble of N atoms coupled to the cavity field the coherent interaction is enhanced by N1/2 and the so-called collective strong coupling regime is reached, when the collective coupling rate gN=g N1/2 exceeds ? and ?.
Recently we could report on the first realization of the collective strong coupling regime with a ensemble of laser cooled ions interacting with the light field of an optical cavity [8].

Our setup consists of a linear rf ion trap incorporating a 12 mm long optical cavity with a moderate finesse of F~3000 along the rf field free axis [9]. Through the use of isotope-selective photoionization, it is possible to produce in situ ion Coulomb crystals containing more than 105 calcium ions of various isotopes and with extension of up to ~4 mm along the cavity axis [9]. The number of ions prepared in a specific magnetic substate of the metastable 3d2D3/2 level of 40Ca+ within the TEM00 cavity mode-volume can correspondingly reach several thousands.
In our setup, we trap and cool 40Ca+ ions in sufficient number to access the collective strong coupling regime, where the collective coupling, gN1/2, exceeds both the dipole decay rate, ?, and the cavity decay rate, ?. By controlling the trapping parameters and the number of trapped ions, we can control the number of ions interacting with the optical light field in the cavity and by this fine tune the coupling strength.
The collective strong coupling regime manifests itself most dramatically via the vacuum Rabi splitting, that results from the oscillatory exchange of excitation between ions and cavity field.
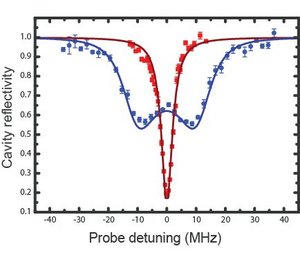
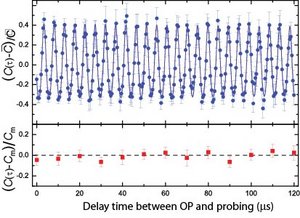
Additionally, we measure the temporal coherence of collective Zeeman sub-states in the 3d3 D3/2-level by induced Larmor precession. The measured coherence times are of the order of the best reported values for single ions in equivalent magnetic field sensitive states.
Our results make the system a promising candidate for the realization of various quantum information devices, including quantum repeaters and quantum memories.
[1] M. A. Nielsen and I. L. Chuang "Quantum Computation and Quantum Information" (Cambridge Univ. Press, 2000).
[2] J. I. Cirac, P. Zoller, H.J. Kimble and H. Mabuchi. "Quantum state transfer and entanglement distribution among distant nodes in a quantum network", Phys. Rev. Lett. 78, 3221–3224 (1997).
[3] M. Fleischhauer, S. F. Yelin, and M. D. Lukin. “How to trap photons? Storing singlephoton quantum states in collective atomic excitations”, Opt. Comm. 179, 395–410 (2000).
[4] D.J. Wineland, J. C. Bergquist, W. M. Itano, J. J. Bollinger and C. H. Manney. "Atomic-ion Coulomb clusters in an ion trap", Phys. Rev. Lett. 59, 2935–2938 (1987).
[5] M. Drewsen, C. Brodesen, L. Hornæker, J. S. Hangst, J. P. Schiffer, ”Large ion Coulomb crystals in a linear Paul trap”, Phys. Rev. Lett. 81, 2878 (1998).
[6] P. Herskind, A. Dantan, M. B. Langkilde-Lauesen, A. Mortensen, J. L. Sørensen and M. Drewsen. ”Loading of large ion Coulomb crystals into a linear Paul trap incorporating an optical cavity”, Appl. Phys. B 93, 373 (2008).
[7] S. Haroche and J. M. Raimond. "Exploring the Quantum: Atoms, Cavities and Photons" (Oxford Univ. Press, 2006).
[8] P. F. Herskind, A. Dantan, J. P. Marler, M. Albert and M. Drewsen.
"Realization of collective strong coupling with ion Coulomb crystals in an optical cavity",
Nat Phys. Vol. 5, 494-498 (2009).
[9] P. Herskind, A. Dantan, M. B. Langkilde-Lauesen, A. Mortensen, J. L. Sørensen, M. Drewsen. ”Loading of large ion Coulomb crystals into a linear Paul trap incorporating an optical cavity”, Appl. Phys. B 93, 373 (2008).