


Fotometri af Kuglehobe
Hertzsprung-Russell Diagramer
Eksamens projekt i Tenerife kurset
Mikael J. Jørgensen
I starten af 1900 tallet, havde astronomer endelig fået lavet utroligt mange målinger af stjerners egenskaber, såsom deres relative magnitude, spektral klasser, afstande, og positioner på himlen. I 1665 havde den tyske amatør astronom Abraham Ihle observeret den første kuglehob (M22). Den første til at opløse en kuglehob var Charles Messier (M4). Dog var det først omkring 1914 der begyndte at ske en større undersøgelse af disse objekter. Siden da er det gået stærkt, siden at kuglehobe har vist sig at kunne bruges inden for mange områder af den moderne astronomi, fra god gammeldags observationel astronomi, til kosmologi. I dette projekt håber jeg at vise at selv relativt simple observationer stadig kan producere store mængder af god information om kuglehobe, ved hjælp af Hertzsprung-Russell Diagramer.
University of AarhusMikael J. Jørgensen
Nov. 2006
Introduktion
I dette afsnit vil jeg kort introducerer hvad kuglehobe egentligt er, og hvilke fysiske karakteristika de har. Jeg vil også forklare kort hvad et Hertzsprung-Russell Diagram er og noget af alt den fysik man kan trække ud af det.
Derefter vil jeg beskrive de observationelle forhold der har gjort sig gældende under mine egne observationer af disse, og derefter gå vidre til selve data behandlingen.
Kort om Kuglehobe
En kuglehob er som navnet hentyder en stor samling af stjerner der ser ud til at have en sfærisk geometri. Der findes også andre typer af hobe, kaldet åbne hobe. En af de mest kendte på den nordlige himmel er syvstjernen. Forskellen mellem disse to typer er enorm. Kuglehobe består gerne af flere hundrede tusinde stjener, kompakt pakket sammen i en kugle. Mens åbne hobe gerne kun kommer op på nogle få tusinde stjerner, og ikke har nogen general struktur. Det som de begge to har tilfælles er at hele system kan ses som et gravitationelt bundet system. dvs. mens de indviduelle stjerner har egenbevægelse, så bevæger hoben som helhed sig også.![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) Dette har sammen med målinger af stjernetåger, givet gode indblik i hvordan mælkevejen opfører sig dynamisk. Det som umildbart gør kuglehobe specielle er dog at de består af mange stjerner, så alle er blevet dannet på ca. samme tid, ud af det samme matriale. Dette betyder at man ved at observere kuglehobes spektra, kan få direkte information om hvad den kemiske sammensætning af mælkevejen var da de blev dannet. Som et laboratorie for stjene udvikling har kuglehobe også spillet en meget central rolle. Siden man har enormt mange stjerner med samme start betingelser, så er det muligt at teste sine teoretiske modeller meget præcist. Siden afh. af hvor en stjerner er i dens udvilking så vil den være forskellige steder i Hertzsprung-Russell Diagramet.
Dette har sammen med målinger af stjernetåger, givet gode indblik i hvordan mælkevejen opfører sig dynamisk. Det som umildbart gør kuglehobe specielle er dog at de består af mange stjerner, så alle er blevet dannet på ca. samme tid, ud af det samme matriale. Dette betyder at man ved at observere kuglehobes spektra, kan få direkte information om hvad den kemiske sammensætning af mælkevejen var da de blev dannet. Som et laboratorie for stjene udvikling har kuglehobe også spillet en meget central rolle. Siden man har enormt mange stjerner med samme start betingelser, så er det muligt at teste sine teoretiske modeller meget præcist. Siden afh. af hvor en stjerner er i dens udvilking så vil den være forskellige steder i Hertzsprung-Russell Diagramet.![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) I kuglehobe har man netop mange stjerner der er i forskellige stadier af deres udvikling, pga. disse stjerners forskellige start masse.
I kuglehobe har man netop mange stjerner der er i forskellige stadier af deres udvikling, pga. disse stjerners forskellige start masse.![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) Derved forventer man kun at se gamle røde stjerner, hvilket også er det man gør. Dette spiller en meget central rolle når man skal observere kuglehobe, som jeg beskriver i afsnit 2.4
Derved forventer man kun at se gamle røde stjerner, hvilket også er det man gør. Dette spiller en meget central rolle når man skal observere kuglehobe, som jeg beskriver i afsnit 2.4
Hertzsprung-Russell Diagramer
Som jeg nævnte i prefacen, så var der i starten af 1900 tallet ikke nogen systematisk måde at behandle alle de data man havde om stjerner. Dette ændrede sig omkring 1910 da den danske astronom Ejnar Hertzsprung og den amerikanske Henry Norris Russell uafh. af hinanden opdagede at når man plottede den absolute magitude eller luminositen mod farven eller temperaturen af stjener, så fik man en meget karakteristisk udsende graf.
På denne graf var det tydeligt at se at tungere og varmere stjerner lå til venstre mens at de store røde ikke så varme stjerner lå til højre.![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) Det mest karakteristiske var dog at næsten
Det mest karakteristiske var dog at næsten 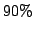 af alle stjernerne lå langs diagonalen. I de efterfølgende år, som der kom computere og flere observationer, så blev det klart at forskellige positioner på et HR-diagram svarede til forskellige steder i en stjernes udvilking. Det blev også klart at afh. af den kemiske sammensætning så ville stjernerne også ligge forskelligt.
af alle stjernerne lå langs diagonalen. I de efterfølgende år, som der kom computere og flere observationer, så blev det klart at forskellige positioner på et HR-diagram svarede til forskellige steder i en stjernes udvilking. Det blev også klart at afh. af den kemiske sammensætning så ville stjernerne også ligge forskelligt.
Observationelle forhold
Når man vil observere kuglehobe, så er der nogle få centrale ting der spiller ind. Helt banalt så er det enste man skal gøre ``bare'' at tage en masse billeder af hoben. Virkeligheden er dog ikke så venlig at dette er det eneste der skal til. I den virkelige verden, må man leve med at man, for det meste, er nød til at observere fra jorden, og dvs. at det lys der modtages skal igennem atmosfæren.I værste tilfælde tillades dette ikke pga. absorption, og i bedste tilfælde så gør lufturoen at ens billeder ikke bliver så skarpe som de kunne være. Derud over er der ikke noget der hedder et perfekt teleskop med perfekt optik. I dag benyttes CCDer i næsten alle teleskoper og små defekter som udlæse støj i disse, spiller også en role mht. til kvaliteten af det endelige billede. Ud over disse jord nære problemer så er det også en kendsgærning at der i rummet findes støv og andre ting der kan være med til at absorbere eller sprede lyset, dette kan der, i modsætning til de andre ting, dog ikke gøres noget ved!
Atmosfæren kan man kompensere for ved at vælge at observere i filtre hvor der er lav absorbtion, og lufturo kan man delvist undgå ved at bruge adaptiv optik. CCD problemet kan næsten fjernes ved at køle CCDen ned til meget lave temperaturer og ved at bygge dem bedre.
Mine Observationer
I dette kapitel vil jeg kort gennemgå de ting der gjorde sig gældende for de observationer jeg har lavet. Her vil jeg også gennemgå lidt om filtre og andre observationelle aspekter.
Observatoriet og teleskopet
Teleskopet der er blevet brugt til dette projekt, er en del Observatorio del Teide som er en samling af forskellige teleskoper nær ved toppen af Izaña (Tenerife), i en højde af ca. 2400m. Teleskopet er IAC´s![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) IAC80 som er et 80cm Cassegrain spejl teleskop. I stedet for at gennemgå alle detaljer om teleskopet, vil jeg blot henvise til observatoriets hjemmeside
IAC80 som er et 80cm Cassegrain spejl teleskop. I stedet for at gennemgå alle detaljer om teleskopet, vil jeg blot henvise til observatoriets hjemmeside![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) for mere information, da det ikke er hovdeformålet med dette projekt.
for mere information, da det ikke er hovdeformålet med dette projekt.
CCDen og feltet
CCDen![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) har en størrelse på 2048x2048 pixel med et felt på ca. 10'x10'. Information om udlæse støj og andre tekniske detaljer ligger tilgængeligt via. observatoriets hjemmeside. Efter observationerne i Tenerife stod jeg med billederne. Det første skridt var så at få flatfeltet disse, og trukket bias fra. Flatfeltning er beregnet til at finde følsomheds fejl i CCDen, så man undgår at den får for mange eller for få photon tællinger forskellige steder i billedet. Bias er for at trække systematiske baggrunds fejlkilder fra billedet som stammer fra CCDen og elektroniken der styre den. Når alt dette er gjort så har man essentielt et klart billede som ikke indeholder andet end de photoner man har modtaget.
har en størrelse på 2048x2048 pixel med et felt på ca. 10'x10'. Information om udlæse støj og andre tekniske detaljer ligger tilgængeligt via. observatoriets hjemmeside. Efter observationerne i Tenerife stod jeg med billederne. Det første skridt var så at få flatfeltet disse, og trukket bias fra. Flatfeltning er beregnet til at finde følsomheds fejl i CCDen, så man undgår at den får for mange eller for få photon tællinger forskellige steder i billedet. Bias er for at trække systematiske baggrunds fejlkilder fra billedet som stammer fra CCDen og elektroniken der styre den. Når alt dette er gjort så har man essentielt et klart billede som ikke indeholder andet end de photoner man har modtaget.
Filtre
En af de ting der er mest vigtig i observationel astronomi er filtre, siden det er filteret der afgør hvilket bølgelængde område der er størst følsomhed overfor. Dette er meget vigtigt afh. af hvad det er man observere. Et meget godt eksempel på dette er den såkaldte mørke plet![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) , som hvis man bruger et visuelt filter så ser man blot en stor sort stjerneløs klat. Men vælger man et infrarødt filter, så ser man lige pludselig at der blot er tale om en meget tæt støv sky og der er stjerner bagved.
, som hvis man bruger et visuelt filter så ser man blot en stor sort stjerneløs klat. Men vælger man et infrarødt filter, så ser man lige pludselig at der blot er tale om en meget tæt støv sky og der er stjerner bagved.
Figure 2.1:
Transmissions kurver for Johnson filtrene U B V R I
![\includegraphics[width=0.70\textwidth]{fil081.eps}](img2.gif) |
Det som figur 2.1 viser er transmissions evenen som funktion af bølgelængde, transmission er i 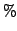 og bølgelænden er er i ångstrøm. Fortolkningen af denne graf er simpel nok, jo højrer tranmission, jo flere photoner ved en given bølgelængde slipper igennem filteret. Det skal vise sig at dette har meget stor indflydelse på fortolkningen af formen af HR-diagramer når man plotter dem i forskellige farver. De filtre som er blevet brugt i mine observationer, er I R V og B.
og bølgelænden er er i ångstrøm. Fortolkningen af denne graf er simpel nok, jo højrer tranmission, jo flere photoner ved en given bølgelængde slipper igennem filteret. Det skal vise sig at dette har meget stor indflydelse på fortolkningen af formen af HR-diagramer når man plotter dem i forskellige farver. De filtre som er blevet brugt i mine observationer, er I R V og B.![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) På observatoriets hjemmeside kan man slå de eksakte transmissions kurver op for de filtre, men de er ens siden filter typen på teleskopet er de samme Johnson filtre der er vist på figur 2.1.
På observatoriets hjemmeside kan man slå de eksakte transmissions kurver op for de filtre, men de er ens siden filter typen på teleskopet er de samme Johnson filtre der er vist på figur 2.1.
Objekterne
Der blev taget billeder af 3 kuglehobe, M2, M15 og NGC7492. Information om disse 3 kan findes i W.E. Harris' database for kuglehobe. I stedet for at smide tal op, vil jeg i stedet forklare de hovdetræk som er vigtige for observationerne.
M2
M2 som også går under NGC7089, ligger små
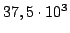 ly væk har en tilsyneladende visuel magnitude på ca. 6, og har en declination der svare ca. til himmel ækvatoren (
ly væk har en tilsyneladende visuel magnitude på ca. 6, og har en declination der svare ca. til himmel ækvatoren (
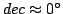 ). Dette var en af grundene til at den blev valgt, siden den ville ligge højt på himlen set fra Tenerife, og derved ville seeingen blive bedre. M2 er ca. 175 ly i diameter, hvilket betyder en udstrækning på himel på ca. 10'. Mere detaljeret undersøgelser har vist at den nok nærmere fylder ca. 15' i stedet. Dette betyder at største delen af de stjerner der er i feltet vil tilhører hoben og ikke være for eller baggrunds stjerner.
). Dette var en af grundene til at den blev valgt, siden den ville ligge højt på himlen set fra Tenerife, og derved ville seeingen blive bedre. M2 er ca. 175 ly i diameter, hvilket betyder en udstrækning på himel på ca. 10'. Mere detaljeret undersøgelser har vist at den nok nærmere fylder ca. 15' i stedet. Dette betyder at største delen af de stjerner der er i feltet vil tilhører hoben og ikke være for eller baggrunds stjerner.
M15
M15 er ca. lige så lange væk som M2,
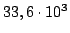 ly har ca. samme tilsyneladende magnitude, på ca. 6. I modsætning til M2 ligger M15 længre oppe på den nordlige himmelkugle, og derved også lidt højrer på himlen end M2 set fra Tenerife. Dette ses også i det billeder der er blevet taget, at seeingen generelt er bedre på billederne af M15. I størrelse så er M15 også større end M2, og det er også den mest tæt pakket af alle kuglehobe i mælkevejen, som vil sige der er lidt flere stjener at få data fra.
ly har ca. samme tilsyneladende magnitude, på ca. 6. I modsætning til M2 ligger M15 længre oppe på den nordlige himmelkugle, og derved også lidt højrer på himlen end M2 set fra Tenerife. Dette ses også i det billeder der er blevet taget, at seeingen generelt er bedre på billederne af M15. I størrelse så er M15 også større end M2, og det er også den mest tæt pakket af alle kuglehobe i mælkevejen, som vil sige der er lidt flere stjener at få data fra.
NGC7492
NGC7492 blev valgt fordi den var den eneste anden kuglehob som stod højt nok på himlem og som kunne ses overhovedet fra Tenerife i den tid vi var dernede. Det mest karakteristiske ved den er umildbart at den ligger meget længre væk, og derved ikke er det ikke muligt at opløse den så godt som de andre.
Observationerne
De billeder der er blevet brugt i det her projekt, er blevet taget natten d.26 og d.27 august 2006. I alt er der behandlet 84 billeder, 40 af M2 og 44 af M15. De få billeder der blev taget af NGC7492 har som sagt vist sig ikke at være lige så godt opløst som de andre, så disse er ikke blevet behandlet. Både M2 og M15 er blevet optaget i B V R og I filtrene, dog er langt de fleste målinger blevet udført i B og I. Der er blevet brugt følgende eksponeringstider i hvert filter.
|
Filter |
Tid/s |
|
|
I |
120 |
|
| R |
120 |
|
| V |
180 |
|
| B |
260 |
|
|
|
|
Det ses at der er en klar stigning i eksponeringstid når der bruges filtre der er mere følsome i den blå del af spektret. Grunden til dette ligger i fysiken bag det lys der modtages. Stjernerne der observeres antages at være perfekte sort legmer, dvs. at de følger Stefan-Boltzmans og Wiens forskydnings lov. Derfor har de en karakteristisk kurve som er afh. af overflade temperaturen af stjernen. På figur 2.2 ses forskellige kurver for forskellige overflade temperature. Hvis denne figur sammenlignes med figur 2.1 så ses det, hvis man f.eks. tager I filteret at det ikke rammer maxima for 5500K kurven. Dog rammer den 3500K kurven meget tætter på. Dette betyder kort og enkelt at der udsendes flere photoner i det givne bølgelængde område, og filteret gør at det også er her der modtages flest. Vælger man dog et B filter og observere en 3500K stjerne så udsendes der ikke lige så mange photoner og derfor skal man observere i længre tid for at få samme antal tællinger.
Figure 2.2:
Sortlegme kurver for forskellige overflade temperature
![\includegraphics[width=0.50\textwidth]{black.eps}](img7.gif) |
Seeing
Mht. seeing![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) så har billederne af M15 i middel ca. 2.74''. De bedste billeder har ca. 2.0'' for både M2 og M15. Der er ikke lavet nogen undersøgelse af dette for NGC7492.
For både M2 og M15 var de målinger der blevet taget først på ugen de bedste, i det at vejr forholdne var meget bedre. Som tiden gik kom der dog en masse støv ind fra Sahara som har haft en indflydelse. Derud over indgår der i begge billede serier billeder som er blevet taget tidligt på morgenen hvor objekterne var meget lavere på himlen.
så har billederne af M15 i middel ca. 2.74''. De bedste billeder har ca. 2.0'' for både M2 og M15. Der er ikke lavet nogen undersøgelse af dette for NGC7492.
For både M2 og M15 var de målinger der blevet taget først på ugen de bedste, i det at vejr forholdne var meget bedre. Som tiden gik kom der dog en masse støv ind fra Sahara som har haft en indflydelse. Derud over indgår der i begge billede serier billeder som er blevet taget tidligt på morgenen hvor objekterne var meget lavere på himlen.
HR-diagramer
I dette kapitel, vil jeg kort beskrive hvad der er relevant at se efter i et HR-diagram, og derefter beskrive metoden hvorpå at jeg har lavet mine egne HR-diagramer. Til sidst, vil jeg fokusere på fortolkningen af disse data, og sætte dem ind i et større perspektiv.
Generelt om HR-diagramer
Man kan vise et HR-diagram på mange forskellige måder, men den generelle form er altid den samme. Op ad y-aksen bruger man gerne luminositeten, eller den absolute magnitude. mens at man ud af x-aksen plotter temperatur, eller farve. Nogle gange bruger man også stjerners spektrale klasse![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) med O stjerner til venstre og M til højre. På figur 3.1 ses et eksempel ud fra stjerner nær ved solen. Det som er mest tydeligt når man ser på figur 3.1 er selve hovdeserien, som er det sted hvor stjerner tilbringer det meste af deres liv, så det er ikke så mystisk at finde det største antal af stjerner der. Den anden prominente struktur er kæmpegrenen som er de stjerner der er gået fra at forbrænde hydrogen til at forbrænde helium. Jeg kommer tilbage til hvorfor formen af dette HR-diagram ikke er det samme som dem jeg producere for M15 og M2.
med O stjerner til venstre og M til højre. På figur 3.1 ses et eksempel ud fra stjerner nær ved solen. Det som er mest tydeligt når man ser på figur 3.1 er selve hovdeserien, som er det sted hvor stjerner tilbringer det meste af deres liv, så det er ikke så mystisk at finde det største antal af stjerner der. Den anden prominente struktur er kæmpegrenen som er de stjerner der er gået fra at forbrænde hydrogen til at forbrænde helium. Jeg kommer tilbage til hvorfor formen af dette HR-diagram ikke er det samme som dem jeg producere for M15 og M2.
Figure:
Et detaljeret HR-diagram af 22000 stjerner fra Hipparcos kataloget og 1000 fra Gliese kataloget af nærvedliggende stjerner.
![\includegraphics[width=0.50\textwidth]{HRD.eps}](img8.gif) |
Fotometri af kuglehobe
Efter flatfelt og bias er trukket fra alle billeder så kan der laves fotometri på dem. Til dette formål bruges fotometri algoritmerne Daophot og Allstar. Detaljer om indstillinger i dette program kan findes i deres manual og jeg vil ikke gå mere ind på dem da det ikke er relevant for dette projekt. I stedet vil jeg kort beskrive beskrive en gennemgang af Daophot og Allstar.
- Først loades billedet der skal behandles ind i programmet.
- Derefter benytter Daophot en find algoritme som forsøger at bestemme hvor mange stjerner der er på et givet billede.
- Derefter findes værdier for magnituderne ved at lave ``Concentric Aperture photometry''. Denne process kan beskrives kort, som at man vælger en stjerne, og så lægger man en ydre og en indre cirkel sådan så den indre kun lige rør kanten af hvor stjernen er. Dette bliver så det et mål for den lokale himmel baggrund. Efter det ligges der andre cirkler inden for den indre af de to jeg lige nævnte. Herefter bliver der så talt photoner inde fra og ud, og baggrunde bliver trukket fra. Dette photon tælle tal bliver så lavet om til en magnitude.
- Herefter udvælger man de bedste stjerner den har fundet. Disse stjerner vil så blive brugt til at lave PSFen
![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) som derefter vil blive brugt på alle andre stjerner. PSFen er kort fortalt en kombination af en analytisk kurve (f.eks. en gauss kurve) og det som er til overes når kurven fittets til stjernen.
som derefter vil blive brugt på alle andre stjerner. PSFen er kort fortalt en kombination af en analytisk kurve (f.eks. en gauss kurve) og det som er til overes når kurven fittets til stjernen.
- Efter alt dette er gjort så køres Allstar hvilket er en iterativ algoritme som analysere de stjerner man har fundet.
- Når denne proces er gjort på alle billeder, så har man en masse individuelle positioner og magnituder. Ved at bruge rutinerne Match og Master kan man få kombineret alle disse data til en samlet fil som man så kan begynde at bearbejde vha. IDL.
Kalibering af data
Efter at have kørt Daophot, Allstar, Match og Master på alle billeder har man alle de data der skal bruges. Disse data bliver så processeret i en IDL rutine som jeg har skrevet. Denne rutine vil først indlæse data fra de rigtige steder, derefter indexere dem i de rigtige filtre, udregne farverne. Til sidst vil den så plotte et ukaliberet HR-diagram![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) For at lave de kaliberet HR-diagramer er der blevet skrevet en seperat rutine.
For at lave de kaliberet HR-diagramer er der blevet skrevet en seperat rutine.![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) Det skal siges at der kun er lavet kalibrering for M15 i B V og I filtrene, fordi der ikke fandtes nok standard stjerner nok i R filteret for M15, og slet ikke fandets nok i nogle af filtrene for M2
Det skal siges at der kun er lavet kalibrering for M15 i B V og I filtrene, fordi der ikke fandtes nok standard stjerner nok i R filteret for M15, og slet ikke fandets nok i nogle af filtrene for M2![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) . Kalibreringen går ud på at man konvertere fra mine magnituder til dem som er brugt i standard systemet.
Metoden til at gøre dette er at man først finder alle standard stjernerne i feltet, ud fra dem som Stetson har i sit katalog. Derved har man standard magnituder for stjernerne fra Stetson, og en observeret magnitude fra billedet. Generelt har man relationen 3.1 mellem den observeret og standard magnituden givet ved.
. Kalibreringen går ud på at man konvertere fra mine magnituder til dem som er brugt i standard systemet.
Metoden til at gøre dette er at man først finder alle standard stjernerne i feltet, ud fra dem som Stetson har i sit katalog. Derved har man standard magnituder for stjernerne fra Stetson, og en observeret magnitude fra billedet. Generelt har man relationen 3.1 mellem den observeret og standard magnituden givet ved.
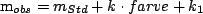
Hvilket blot er en ligningen for en ret linje. Konstanterne k og k1 kan findes ud fra lineær fitning idet at farven blot er to standard magnituder trukket fra hinanden og disse kender man for standard stjernerne. Ud fra dette kan man så lave et ligning system med 3 ligninger, et for hvert filter.
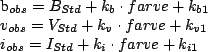
Metoden er nu rimeligt ligetil. Man finder konstanterne for de 3 filtre ud fra standard stjernerne. Resultatet fra dette er vist på figur 3.2
Figure:
Resultatet af de linære fit. Der er et offsæt på +5 og +10 på V og B. Der er en mindre fejl ved V filtert, som det er beskrevet i teksten.
![\includegraphics[width=0.70\textwidth]{obscal.ps}](img12.gif) |
Nu står man dog med problemet at man ikke kender farven for en vilkårlig stjerne i feltet. Dette er der dog råd mod for ved at se på ligning 3.2 ser man at når man kender konstanterne så er den eneste ukendte farven og standard magnituden. Dog er farven ikke andet en differensen mellem to standard magnitude, så ved at trække de to ligninger fra hinanden får man kun farven som ubekendt.
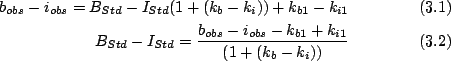
Dvs. for en vilkårlig felt stjerne kan man regne dens kaliberet farve ud. Når man så kender den kan man bruge den til at regne resten af de kaliberet magnituder ud i ligning 3.2.

Som det ses på figur 3.2 så ses det at udregningerne stemmer findt overens med data i alle 3 filtre, dog skal det siges at der er en mindre fejl ved V filteret, i det at koden gav de forkerte værdier for hældnings koefficenten. Denne fejl ser ud til ikke at være helt fjernet, og jeg har ikke haft tid til at undersøge det nærmere. Men jeg vender tilbage med et konkret bevis på at der er noget galt senere.
HR-diagram analyse
Jeg vil nu gå i gang med at se på de resultater der er kommet ud af databehandlingen. Til dette formål vil jeg hovdesageligt forkusere på M15, siden den var den eneste der kunne kaliberes. Og fordi som nævnt i afsnit 2.3.2 pga. M15´s højrere placering på himlen så var seeingen bare bedre. Dette ses mest tydeligt når man sammenligner billeder af M15 og M2. Hos M15 kan man tydeligt![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) se turnoff, mens at man på M2 kun lige kan skimte det på b-i billederne.
se turnoff, mens at man på M2 kun lige kan skimte det på b-i billederne.
M2 og NGC7492
Som sagt var der ikke nogen standard stjener til at kaliberer M2 efter, men de ukaliberede billeder kan ses på figurne A.6,A.7 og A.8 i appendix. Selv om NGC7492 ikke bliver analyseret i samme detalje som M15 her så er der alligevel lagt et enkelt HR-diagram af den med i figur A.9. Man kan svagt se den røde kæmpegren og horizontal grenen, men langt de fleste stjerner ligger ved hvad der måske burde være turnoff, men precisionen af disse data er ikke god nok til at man kan udtale sig meget mere end det.
M15
Før kaliberingen kan man også godt lave HR-diagramer baseret på de observerede magnituder. På figurne A.3,A.4 og A.5 i appendix er lagt de ukaliberet billeder ud. De kaliberet HR-diagrammer kan findes i figur A.1. For at illusterer den mærkante forskel der er på de kaliberet og ukaliberede billeder så er figur A.2 lagt med som sammenligning. Denne forskel, selv om den ser systematisk ud, har ingen fysisk baggrund. Men er udelukket et produkt af de forskellige tal der er brugt til at udregne magnituderne.
En anden ting der falder i øjene når man sammenligner HR-diagramer i forskellige farver, og akser er at selv om den generelle form![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) så bliver horizontal grenen mere strukket ud når man ser som man går mod større differens i farve. Dette ses tydeligt på figur A.3 som man går fra b-v til b-i. Grunden denne trend kan forklares ved at se tilbage på figur 2.2.
De stjerner der ligger på enden i horizontal grenen er meget varme på overfladen, ca. 20-30000K. Mens at hvis man f.eks tager en kæmpegrens stjerne, så er den relativt kold, kun 3-5000K på overfladen. De to Planck kurver for disse vil være vidt forskellige. Forskellen mellem b og i på en varm planck kurve vil være større end den tilsvarende forskel på en kold. Og derved vil stjernen der er varm blive trukket mere mod den blå ende, mens de kolde mere eller mindre bliver hvor de er.
Denne trend ses også på billederne af M2 og alle de andre figure i forskellige farver, og grunden er den samme som lige er blevet forklaret.
så bliver horizontal grenen mere strukket ud når man ser som man går mod større differens i farve. Dette ses tydeligt på figur A.3 som man går fra b-v til b-i. Grunden denne trend kan forklares ved at se tilbage på figur 2.2.
De stjerner der ligger på enden i horizontal grenen er meget varme på overfladen, ca. 20-30000K. Mens at hvis man f.eks tager en kæmpegrens stjerne, så er den relativt kold, kun 3-5000K på overfladen. De to Planck kurver for disse vil være vidt forskellige. Forskellen mellem b og i på en varm planck kurve vil være større end den tilsvarende forskel på en kold. Og derved vil stjernen der er varm blive trukket mere mod den blå ende, mens de kolde mere eller mindre bliver hvor de er.
Denne trend ses også på billederne af M2 og alle de andre figure i forskellige farver, og grunden er den samme som lige er blevet forklaret.
M15´s alder
En af de interresandte ting ved kuglehobe, er som nævnt i afsnit 1.1 at alle stjernerne er dannet på samme tid. Dvs. at man kan lave stjerne udviklings modeller og ud fra dem lave kurver der forudsiger hvordan en given stjerne burde bevæge sig i et HR-diagram. Disse er kaldet isochroner. På figur 3.3 ses et kaliberet billede, hvor der også er justerede for rødfarvening![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) . Denne justering er den samme som den der er brugt i Harris og Durrel´s artikel, og er givet ved
EB-V(M15)=0.10. Ændringen på y-aksen er fra, at det som er vist på alle andre billeder er afstands moduluet og derved skal dette trækkes fra. Denne værdi er også taget fra Harris og Durrel, og er givet ved
(m-M)V =15.40 for en estimeret afstand til M15 på
. Denne justering er den samme som den der er brugt i Harris og Durrel´s artikel, og er givet ved
EB-V(M15)=0.10. Ændringen på y-aksen er fra, at det som er vist på alle andre billeder er afstands moduluet og derved skal dette trækkes fra. Denne værdi er også taget fra Harris og Durrel, og er givet ved
(m-M)V =15.40 for en estimeret afstand til M15 på
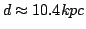 .
.
Figure:
På figuren ses et kaliberet billede med ekstra korektion for rød farvening. Isochronerne er lagt oven på i rækkefølgen første kurve fra venstre svare til 8Gyr. Stjernerne er Stetsons standard stjerner. Det ses tydeligt at der er noget galt med mine data. Tak til Frank Grundahl for isochronerne
![\includegraphics[width=0.70\textwidth]{M15iso.ps}](img16.gif) |
Det som ses er at isochronerne ikke passer helt med min kæmpegren men ligger lidt forskubbet. For at undersøge dette nærmere prøvede jeg også at plotte Stetsons standard stjerner, for at udelukke en fejl i isochron udregningen. Det ses at disse passer meget godt, og at der derved mangler at blive lavet yderligere korrektioner på mine data, og isochronerne er gode nok. Dette bliver dog ikke gjort i dette projekt da det ville blive for omfattende. Dog er det betrykkende at de isochroner der ser ud til at passe bedst ved turnoff, er mellem 10 og 12 Gyr hvilket stadig er mindre end en alder på ca. 13 Gyr estimeret for universets alder via andre kosmologiske metoder.
Center eller felt
En fordel ved denne form for analyse som er brugt i dette projekt, er at den også giver en mulighed for at undersøge de mere kvantitative egenskaber af de orginalle billeder. Hvis man nu f.eks. gerne vil undersøge hvordan fordelingen af stjerner der udgør ens HR-diagram er. Dvs. kommer største delen af dem fra centrum eller fra det omkring liggende felt. Det er værd at huske at M15 er den mest kompakte hob, og derved har langt flere stjerner i centeret. Derved ville det være en rimeligt første approximation at antage at de fleste stammer her fra. På figur 3.4 ses forskellen hvis man kun tager de stjerner der ligger i centrum, og kun dem som ligger ude i feltet.
Figure:
Til venstre er de stjerner fra centeret af M15 som bidrager til HR-diagramet, til højre dem fra feltet.
![\includegraphics[width=0.70\textwidth]{M15center.ps}](img17.gif) |
Det ses tydeligt her at den antagelse er forkert! De stjerner der bidrager er hovdesageligt dem der ligger i feltet. Grunden til dette er også ganske simpel hvis man overvejer det jeg nævnte i afsnit ![[*]](http://icons.uni-x.uni-c.dk/icons.gif/cross_ref_motif.gif) . Selv om der er flere stjerner i centeret, så ligger de så tæt, at seeingen gør man ikke kan enkelt opløse dem. Og derved vil de ikke blive registeret i den simple gennemgang jeg har brugt. Man kunne få lidt flere med hvis man rafinerede de indstillinger man giver til Daophot, men hvis det virkeligt skal blive bedre skal man have adgang til et teleskop med adaptiv optik, eller et rumbaseret teleskop.
. Selv om der er flere stjerner i centeret, så ligger de så tæt, at seeingen gør man ikke kan enkelt opløse dem. Og derved vil de ikke blive registeret i den simple gennemgang jeg har brugt. Man kunne få lidt flere med hvis man rafinerede de indstillinger man giver til Daophot, men hvis det virkeligt skal blive bedre skal man have adgang til et teleskop med adaptiv optik, eller et rumbaseret teleskop.
Sammenligning med andre data
Til dette formål har jeg fundet den artikel jeg allerrede har nævnt af Harris og Durrel. Mange af de resultater som de behandler i deres artikel, er lidt mere dybe gående end det der er blevet behandlet her. Forskellen mellem mine observationer og deres er at de også har lavet en dybe måling af M15, og derved kan de få turn off opløst meget bedre, og få mere af hovdeserien med. Deres bredfelts billeder er dog meget lig med dem som jeg har taget, jeg brugte som sagt en 80cm kikkert, mens de har brugt en 90cm. Det som er værd at lægge mærke til når man sammenligner mine HR-diagramer med deres er at jeg har mange flere kæmpegren og horizontal stjerner med. Det viser sig at både jeg og dem har haft ca. de samme observationelle forhold mht. seeing. De har
1.8''-2.2'' hvor jeg som nævnt i afsnit ![[*]](http://icons.uni-x.uni-c.dk/icons.gif/cross_ref_motif.gif) i middel for M15 har ca 2.74''. Så umildbart ville man forvente at se flere stjerner i deres billeder jvf. den bedre seeing, men jeg tror at grunden til den store forskell ligger i at deres Daophot kørsler har været mere rafineret end mine, og derved har de fået reduceret flere stjerner fra. Dog når man sammenligner med deres endelige resultat hvor de også tager data ind fra andre observationer, så bliver deres horizontal og kæmpegren lige så intens som min. Dog kan jeg sammenligne mine data bedre end blot ved at se på HR-diagramerne. Egentligt har jeg allerede gjort dette på figur 3.3 siden de i deres artikler har stjerner der matcher med Stetsons data.
På figure 3.3 er der et offsæt, men som jeg nævnte tidligiere så var der et problem med V filteret, som åbenbart ikke er blevet rettet helt. For at undersøge om dette var tilfældet, har jeg lavet en tilsvarende sammenligning med I filteret i stedet for. Resultatet heraf ses på 3.5.
i middel for M15 har ca 2.74''. Så umildbart ville man forvente at se flere stjerner i deres billeder jvf. den bedre seeing, men jeg tror at grunden til den store forskell ligger i at deres Daophot kørsler har været mere rafineret end mine, og derved har de fået reduceret flere stjerner fra. Dog når man sammenligner med deres endelige resultat hvor de også tager data ind fra andre observationer, så bliver deres horizontal og kæmpegren lige så intens som min. Dog kan jeg sammenligne mine data bedre end blot ved at se på HR-diagramerne. Egentligt har jeg allerede gjort dette på figur 3.3 siden de i deres artikler har stjerner der matcher med Stetsons data.
På figure 3.3 er der et offsæt, men som jeg nævnte tidligiere så var der et problem med V filteret, som åbenbart ikke er blevet rettet helt. For at undersøge om dette var tilfældet, har jeg lavet en tilsvarende sammenligning med I filteret i stedet for. Resultatet heraf ses på 3.5.
Figure 3.5:
Sammenligning mellem standard stjerner og mine data. Det ses tydeligt at de matcher.
![\includegraphics[width=0.70\textwidth]{M15isoI.ps}](img18.gif) |
Her på ses det at Standard stjernerne alligevel matcher så det kan konstateres at problemet med V kaliberingen ikke er lykkes. En anden måde at undersøge hvor godt mine data matcher med deres, kunne jeg have taget de punkter de bruger til at lave deres fiducial graf, og plotte dem oven i mine og se hvor meget de afviger. Men dette havde jeg ikke tid til at gøre.
Sammenligning med andre HR-diagramer
Som det ses så er formen af alle HR-diagramerne af både M15 og M2 ens i udformning. Mens at de begge afviger en del fra det som er vist på figur ![[*]](http://icons.uni-x.uni-c.dk/icons.gif/cross_ref_motif.gif) . Grunden til dette er et helt felt i sig selv, men har noget at gøre med metal indholdet i hobene, siden det har vist sig at selv om alle kuglehobe har ca. samme udformning så ændre deres HR-diagramer sig afh. hvor stort et metal indhold der er i dem. Grunden til at det ikke kan ses på M2 og M15 så tydeligt er at de begge to er meget gamle og derved meget metal fattige.
. Grunden til dette er et helt felt i sig selv, men har noget at gøre med metal indholdet i hobene, siden det har vist sig at selv om alle kuglehobe har ca. samme udformning så ændre deres HR-diagramer sig afh. hvor stort et metal indhold der er i dem. Grunden til at det ikke kan ses på M2 og M15 så tydeligt er at de begge to er meget gamle og derved meget metal fattige.![[*]](http://icons.uni-x.uni-c.dk/icons.gif/foot_motif.gif) For et par eksempler på de større modsætninger så vil jeg blot henvise til de to kugle hobe Terzan 5 og Liller 1 som man kan læse om i Ortolani, S et al. som jeg har givet i referencer.
For et par eksempler på de større modsætninger så vil jeg blot henvise til de to kugle hobe Terzan 5 og Liller 1 som man kan læse om i Ortolani, S et al. som jeg har givet i referencer.
Konklusion og diverse
Der er mange andre spændende ting der kunne tilføjes, men det ville være at gå for vidt at skrive om disse også. Der er blevet lavet en hel del HR-diagramer. De mest interresandte er dem af M15, mens at dem som er vedlagt af M2 og NGC7492 også hjælper med at vise nogle vigtige aspekter, så som hvad afstand og seeing gør ved de endelige resultater. Metoden til at vise hvordan man går fra observerede til standard magnituder er blevet gennemgået, og det er forsøgt undersøgt hvorvidt at mine data stemmer overens med andre der er lavet lignende observationer. I den sammenhæng er det også blevet undersøgt hvorvidt mine data kunne bruges til at fastlæge M15´s alder. Det er beklageligt at der ikke har været mere tid til at få ordnet problemet med V filteret. Men alligevel kunne det med lidt god vilje ses at alderen stemmer overens med dem fundet for mere detaljeret undersøgelser. Det er også trist at der ikke har været tid til at lave en konversion fra farve til temperatur, hvilket ville have været mere illustrativ. Jeg kunne blive ved med at nævne ting som ville have været gode også at undersøge, men nogle af de vigtige aspekter er blevet gennemgået i et relativt kvalitativt omfang. Det har været lærerigt at lave dette projekt, men kunne ikke have ladet sig gøre uden hjælp og gode råd fra en hel del personer. Med det på hjerte så som en sidste kommentar, vil jeg gerne takke Frank Grundahl for at være så hjælpsom og tålmodig!
Her i er så alle de HR-diagramer jeg syntes fyldte for meget i teksten.
Figure A.1:
De kaliberet billeder af M15
![\includegraphics[width=0.70\textwidth]{CalM15com.ps}](img19.gif) |
Figure A.2:
De ikke kaliberet billeder som kan sammenlignes med de kaliberet billeder.
![\includegraphics[width=0.70\textwidth]{M15com.ps}](img20.gif) |
Figure A.3:
HR-diagramer af M15 i forskellige B filter kombinationer.
![\includegraphics[width=0.70\textwidth]{M15B.ps}](img21.gif) |
Figure A.4:
HR-diagramer af M15 i forskellige V filter kombinationer.
![\includegraphics[width=0.70\textwidth]{M15V.ps}](img22.gif) |
Figure A.5:
HR-diagramer af M15 i forskellige R filter kombinationer.
![\includegraphics[width=0.70\textwidth]{M15R.ps}](img23.gif) |
Figure A.6:
HR-diagramer af M2 i forskellige B filter kombinationer.
![\includegraphics[width=0.70\textwidth]{M2B.ps}](img24.gif) |
Figure A.7:
HR-diagramer af M2 i forskellige V filter kombinationer.
![\includegraphics[width=0.70\textwidth]{M2V.ps}](img25.gif) |
Figure A.8:
HR-diagramer af M2 i forskellige R filter kombinationer.
![\includegraphics[width=0.70\textwidth]{M2R.ps}](img26.gif) |
Figure A.9:
HR-diagram af NGC7492
![\includegraphics[width=0.70\textwidth]{ngc7492.ps}](img27.gif) |
-
- 1
- Harris, W.E 1996, AJ , 112, 1487
- 2
- J. Dalsgaard : Lecture notes on Stellar Structure and Evolution, 6th edn, 2nd printing (Institute of Physics and Astronomy, University of Aarhus, Denmark)
- 3
- Ortolani, S.; Barbuy, B.; Bica, E. : Astronomy and Astrophysics, v.308, p.733-737 (1996) : NTT VI photometry of the metal-rich and obscured bulge globular cluster Terzan 5
- 4
- Ortolani, S.; Bica, E.; Barbuy, B. : Astronomy and Astrophysics, v.306, p.134 : NTT V, I and Gunn Z colour-magnitude diagrams of Liller 1
- 5
- Patrick R. Durrel , William E. Harris : The Astronomical Journal, Vol:105 nr:4, (1993 april)
-
Hertzsprung-Russell Diagramer
Eksamens projekt i Tenerife kurset
This document was generated using the
LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 1 Tenerife.
The translation was initiated by Soeren Frandsen on 2007-01-01



Soeren Frandsen
2007-01-01
![\includegraphics[width=0.70\textwidth]{fil081.eps}](img2.gif)
![\includegraphics[width=0.50\textwidth]{HRD.eps}](img8.gif)
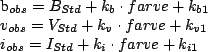
![\includegraphics[width=0.70\textwidth]{obscal.ps}](img12.gif)
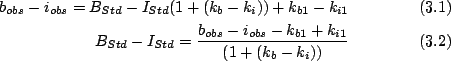
![\includegraphics[width=0.70\textwidth]{M15iso.ps}](img16.gif)
![\includegraphics[width=0.70\textwidth]{M15center.ps}](img17.gif)