Image formation
The imaging system (the telescope) is characterized by its aperture ratio f/D, where f is the focal length and D the diameter. A modern telescope has a small f ratio, which means the telescope is shorter, can be installed in a smaller building and gives a larger concentration of light in the focal plane (see the figure).
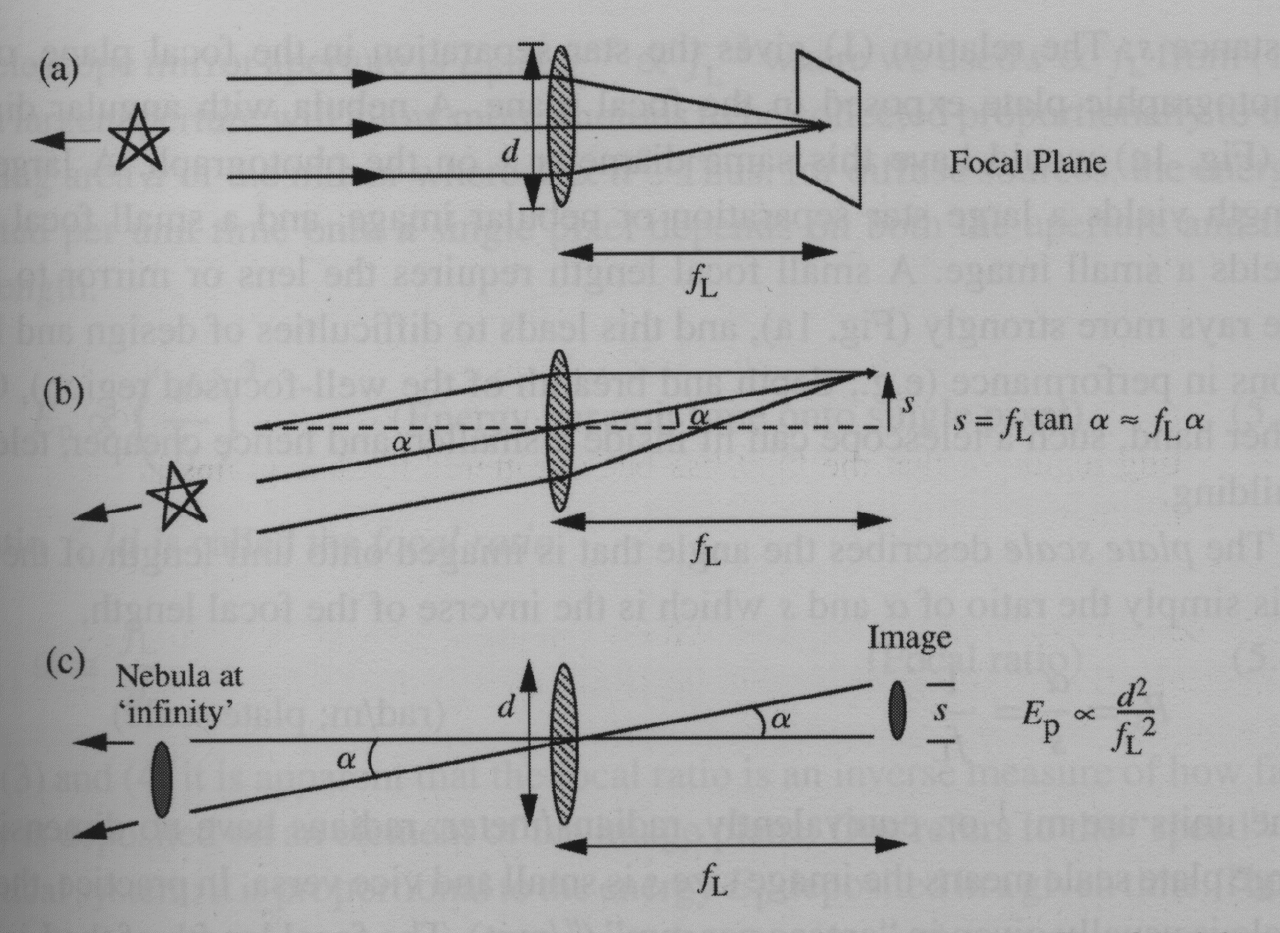
Older telescopes had f/13.5 ratios, whereas new telescopes can have f/6 or even smaller values. This is also called a fast beam.
Telescope systems
Telescopes are constructed in different ways depending on the size, need for instrumentation and wavelength range. The next figure shows various layouts.
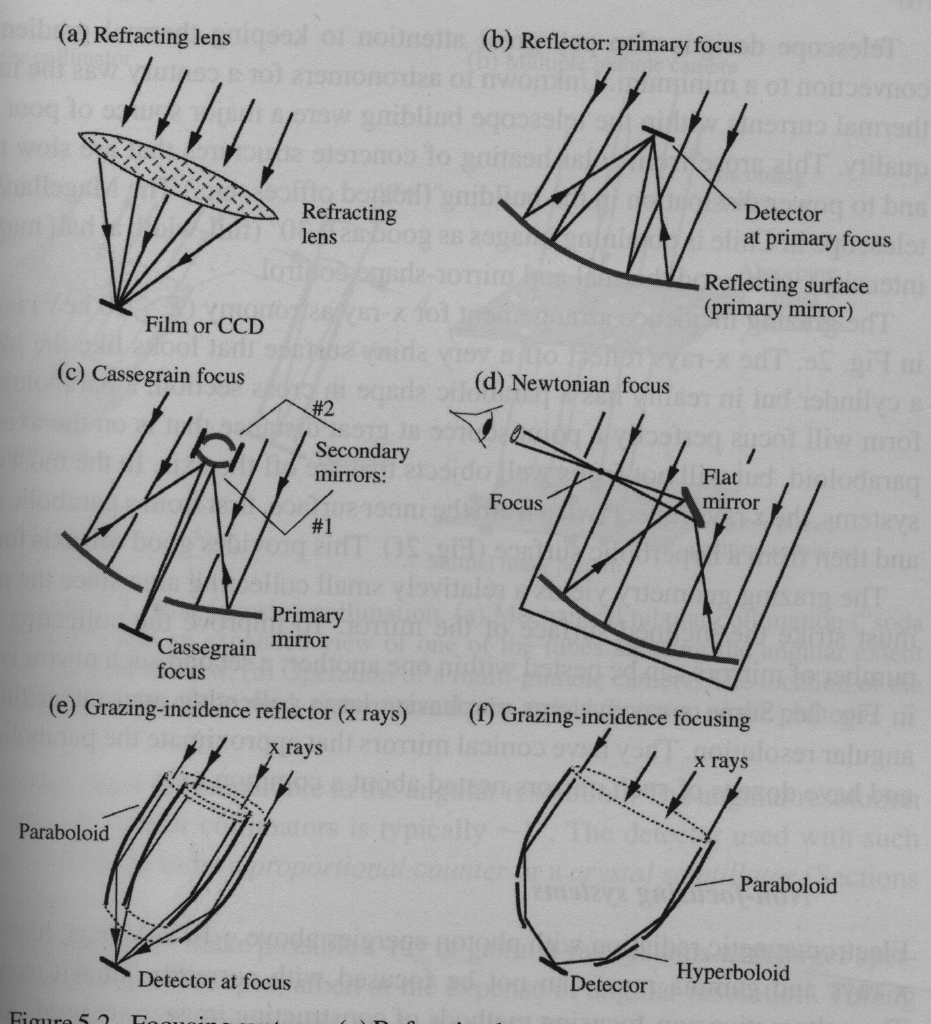
Refractive optics are only used for small telescopes. Most telescopes nowadays have a Cassegrain focus, but for instance the VLT is equipped with two Nasmyth foci. This is not shown in the figure above.
The Very Large Telescope in Chile consists of four telescopes with a mirror diameter of 8m each. One of them is shown here. It is a fairly short telescope.

Danish astronomers have access to all ESO telescopes by submitting applications twice per year. This includes the VLT telescopes. A large portion of time is available on the danish 1.5m telescope, which is housed in a classical dome at the La Silla Observatory.
A complete list of telescopes at La Silla you will find in this Photo Gallery
We also have a large fraction of time (20%) on the 2.5m Nordic Optical Telescope at the Canarian Island La Palma. Here is a corresponding Image Gallery.
Telescope equations
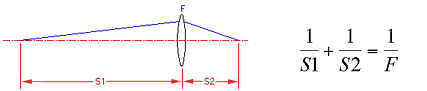
The first equation, which is very basic and often used in optics, is the relation between the distance to the object, the distance to the image and the focal length of a lens
The next equation is called lens makers formula and gives the focal length of a lens with surfaces with curvature radii R1 and R2
1/f = (n-1)(1/R1 - 1/R2)
For a normal bi-concave lens R1 is positive and R2 is negative. R1 corresponds to the first surface that the light meets. n is the refractive index of the glass.
Next we will look at a Cassegrain telescope with a concave secondary mirror
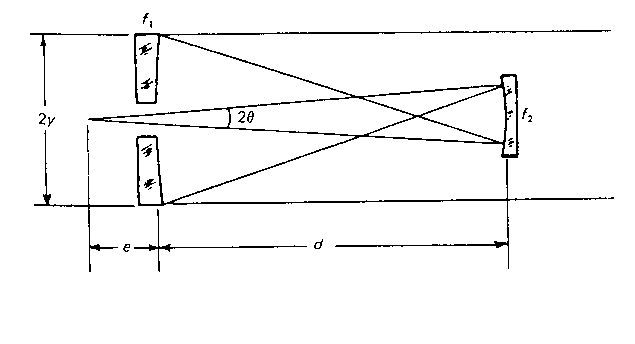
The focal length of this telescope is given by the equation
1/f = 1/f1 + 1/f2 - d/(f1f2)
The distance of the focal point away from the primary mirror e is given by
e = f(f1-d)/f1 - d
which defines the space for mounting instruments, which need to have the detector at the focal point. The focus can be moved by moving the secondary mirror. A change of the distance d leads to a change of the focal position e given by
Δe = (1 + m2)Δd, where m = f1/f2
The focal plane is not a plane for a Cassegrain telescope. It has a curvature radius that depends on the focal length of the mirrors
1/Rc = 1/f1 + 1/f2
where the secondary often is the dominating part.
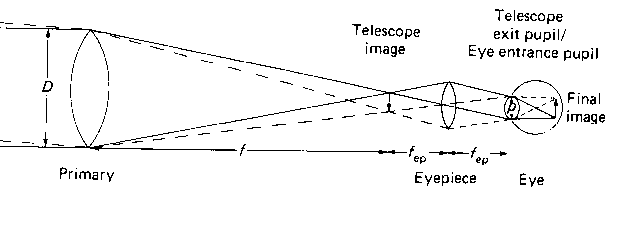
If we look through a telescope we will be using an eyepiece, which should match the telescope pupil given by the size D of the primary mirror to the entrance pupil of the eye, which for a dark adapted eye typically has a diameter of 7 mm. Otherwise some light will be lost. This gives a relation
p = Dfep/ftel
which then with p=7mm leads to a minimum magnification
magn. = ftel/fep = D/7
One can use an eyepiece with a shorter focal length and still get the light in the eye with a larger magnification.
Image scale
The size of the image is determined by the focal length of the telescope. If we have a source on the sky with angular size α then the size on the detector is given by
s = fα
For a given telescope one defines the plate scale as number of arcsec per mm.
Image formation
The diffraction will lead to an image of a point source with a diameter corresponding to
s = 1.22λ/D radians