next up previous
Next: About this document ...

Observationelle Værktøjer


The Echelle grating


The equations


The grating equations is still valid

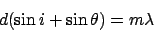\begin{displaymath}d(\sin i + \sin \theta) = m\lambda \end{displaymath} (1)

but due to the tilted surface the angle going into the blaze function is now relative to the socalled blaze angle 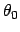$\theta_0$:

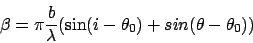\begin{displaymath}\beta = \pi{b \over \lambda}(\sin(i-\theta_0) + sin(\theta - \theta_0)) \end{displaymath} (2)

Also the dispersion relation changes, making the dispersion independent of the spectral order m

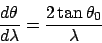\begin{displaymath}{d\theta \over d\lambda} = {2\tan\theta_0 \over \lambda} \end{displaymath} (3)

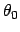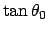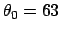Echelle gratings are used at high angles $\theta_0$. They are named after the ratio between width and lengthi or $\tan\theta_0$. A R2 grating is twice as long as wide and is used at angle (the blaze angle) $\theta_0 = 63$ deg.

The orders overlap. The grating equation is fulfilled for several combinations of wavelength 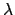$\lambda$ and order m:

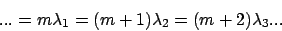\begin{displaymath}...=m\lambda_1=(m+1)\lambda_2=(m+2)\lambda_3... \end{displaymath} (4)

In wavelength the distance between two interference orders becomes

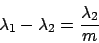\begin{displaymath}\lambda_1 - \lambda_2 = {\lambda_2 \over m} \end{displaymath} (5)


 
next up previous
Next: About this document ...
Soeren Frandsen
2007-03-01