Experiments with ultracold atoms trapped in pools of light allow physicists to explore quantum dynamics of interacting particles with unprecedented control and precision. The nature of these dynamics runs along a spectrum from simple to complex, from controllable to uncontrollable, and from persistent to transitory. Typically, systems with simple, predictable, and stable dynamics are represented by models with straightforward mathematical properties and with all particles having the same mass. This paper presents a model of interacting particles with different masses, which, depending on the initial conditions, can exhibit the full range of dynamical behaviors.

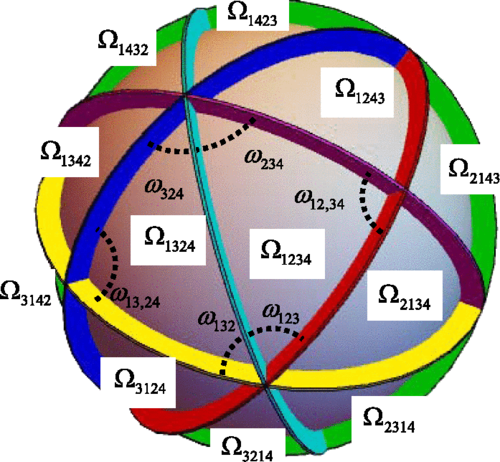
The model describes a few hard quantum particles trapped and bouncing back and forth in a one-dimensional bowl. The key technical insight is realizing that, for example, four particles in one dimension are equivalent (for most quantum-mechanical purposes) to one particle in four dimensions. By moving to this higher-dimensional space and choosing the right coordinates, some symmetries become more obvious and more useful. These symmetries can be used to map the system we are studying onto a simpler model, namely, a single particle bouncing around within a triangle on the surface of a sphere. The shape of the triangle depends on the masses of the particles and their specific order in the trap.

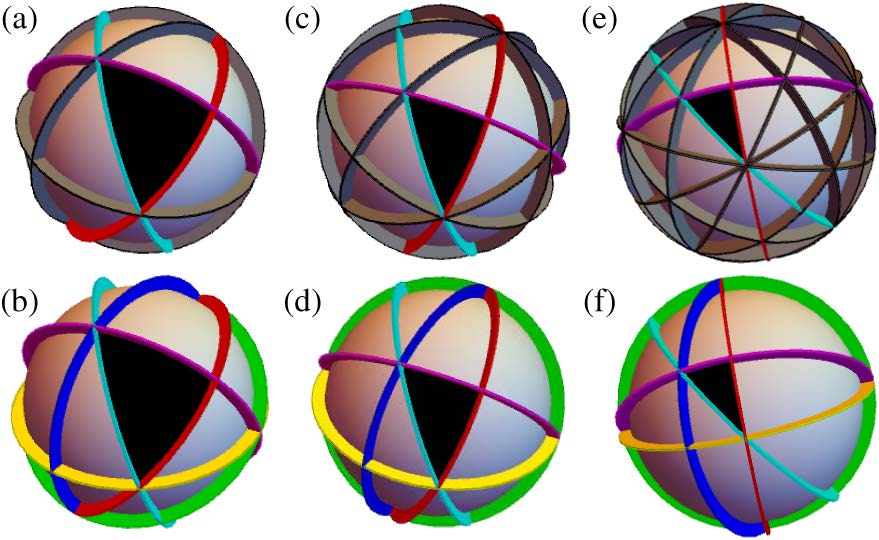
Different mass relations give different shapes of triangles after the transformation

One consequence is that experimentalists will be able to construct systems that are close to integrable systems, which have as many conserved quantities (like energy and momentum) as they have degrees of freedom. These systems may have practical applications because they do not thermalize as fast and they provide unique opportunities for controlling entanglement and coherence, key resources for quantum information processing.

The paper from Physical Review X can be downloaded here