Koordinattransformation giver kvanteløsninger for ulige masser
Vekselvirkende kvantepartikler i et system, hvor masserne er indbyrdes forskellige er notorisk svære at beskrive. I Physical Review X for 10. oktober 2017 beskriver et forskerhold, hvor Nathan Harshman (hovedforfatter), Amin Dehkharghani og Nikolaj Zinner fra IFA deltager, hvordan der kan findes eksakte løsninger til specialtilfælde ved hjælp af en smart transformation af koordinatsæt for særlige masseforhold.
Fanger man ultrakolde atomer i 'fælder' af laserlys kan man studere de kvantedynamiske vekselvirkninger imellem partiklerne med en præcision, som ellers ikke er mulig. De kvantedynamiske forhold kan antage alle mellemværdier fra det enkle til det komplekse, fra det kontrollérbare til det spontane, og fra det blivende til det kortvarige. Typisk studerer man systemer i modeller med simple matematiske egenskaber, hvilket opnås i tilfældet hvor alle partikler har samme masse. I artiklen her præsenteres en model, hvor partiklerne kan have forskellige masser, og, afhængigt af startbetingelserne, hvor de kan opføre sig på alle de mulige måder.
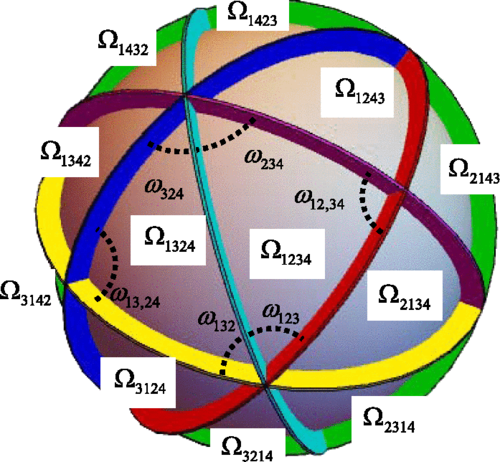
Modellen beskriver nogle få hårde kvantepartikler, som er fangede, og som i en endimensionel skål hopper frem og tilbage. Nøglen til den nye erkendelse er, at for eksempel fire partikler i en dimension opfører sig på samme måde som en partikel i fire dimensioner i de fleste kvantemekaniske henseender. Med det rette valg af koordinater og masseforhold i dette højeredimensionale rum, dukker der nogle meget nyttige symmetrier op. Symmetrierne kan så igen bruges til at afbilde det studerede system i en simplere model: en enkelt partikel, som hopper rundt indenfor en trekant på overfladen af en kugleskal. Ved endnu en smart koordinattransformation kan den sfæriske trekant projiceres ned på et plan. Trekantens nøjagtige form afhænger af partiklernes masse og deres placering i fælden. Beregninger på en sådan enkelt bundet partikel har eksakte løsninger.
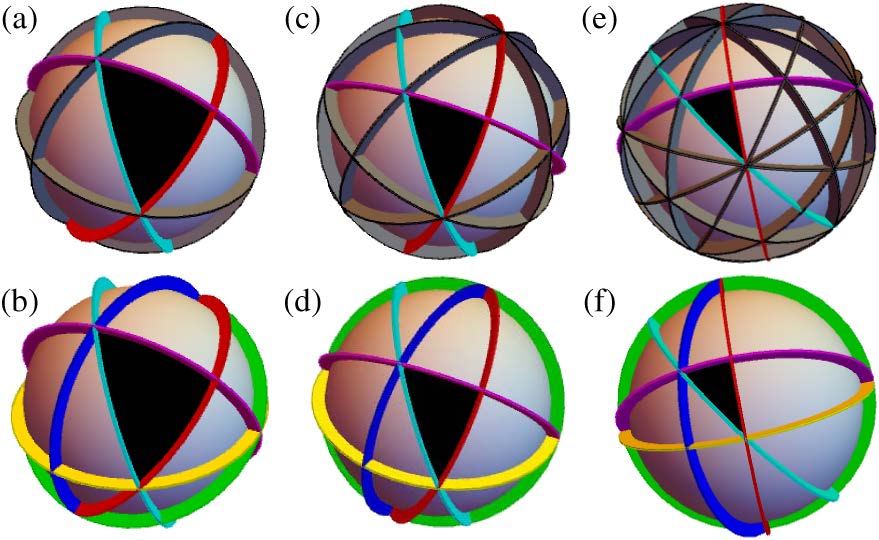
Forskellige masseforhold giver forskellige trekanter efter transformationen
Når man almindeligvis regner på kvantemekaniske systemer sker det ved numeriske tilnærmede beregninger, fordi systemerne er yderst komplicerede, og ikke har generelle eksakte løsninger. Et sæt af eksakte symmetriske løsninger som det fundne er nyttige som 'kalibreringer' af både teoretiske tilnærmede beregningsmodeller, og i eksperimentelle situationer som 'benchmarks' og herfra kan forsøgsbetingelserne så varieres og ny indsigt opnås.
Eksperimentelt vil man kunne tilpasse systemer, som tilnærmer systemer med eksakte løsning såfremt de har lige så mange bevarede egenskaber (såsom for eksempel energi og impuls) som de har frihedsgrader. For at forstå ’frihedsgrader’ hjælper det at tænke på en partikel som kun kan bevæge sig på eksempelvis overfladen af en kugle. Sådan en partikel vil have to frihedsgrader fordi man på kuglen kun har to bevægelsesretninger, eksempelvis langs nord-syd eller øst-vest retningerne. Den slags tilpassede systemer kan have praktiske anvendelser fordi de ikke henfalder nær så hurtigt, og fordi de giver unikke muligheder for at kontrollere vekselvirkning og kohærens - to egenskaber, som er væsentlige for bearbejdning af kvanteinformationer.
